Hvor langt væk kan du se en meteor?
>Jeg får e -mail.
De fleste stiller spørgsmål af forskellige typer, hvoraf de fleste er ret ligetil at besvare (faktisk kan mange blive besvaret ved at google, tip). Men nogle gange får jeg et spørgsmål, der er sværere at besvare, eller endda et, som jeg har undret mig over, men aldrig har fundet ud af at finde ud af.
Så jeg var ret fascineret, da jeg fik et spørgsmål fra Bad Reader Dean Lewis om meteorer. Under Perseid -meteorregn i 2018 var han væk fra sin familie, adskilt af omkring 1.000 kilometer. Hvis han så en meteor, var det muligt, at de kunne se den samme fra deres fjernere lokalitet?
Det korte svar er: Ja! Det lange svar er ... matematik. Fed, sjov matematik.
Og da jeg, når denne artikel er lagt ud, de årlige Geminid -meteorregn i 2018 topper i aften, synes jeg det er passende at finde ud af dette.
tegn på, at din eks vil have dig tilbage
Crash Course Astronomy: Meteorer, Meteoroider og Meteoritter, Oh My!
Hvis Jorden var helt flad, så kunne du i princippet se en meteor helt til enhver kant af Jorden. Så længe du er over jorden, selv en lille smule, så når din sigtelinje hver kvadratcentimeter af planeten på din side, så hver meteor er synlig for alle. I virkeligheden er luften ikke helt gennemsigtig, så i en vis afstand kigger du igennem så meget lort, at du ikke kan se noget.
Jorden er imidlertid ikke flad. Helt seriøst! Det er rundt. Og atmosfæren omgiver den som en skal, bliver tyndere med højden og til sidst petering ud; at højden afhænger af din definition af rum. Vi kan dog snyde lidt, da vi kender videnskaben: Meteorer som dem i byger har en tendens til at brænde op omkring 100 kilometer over jorden. Den højde afhænger af mange ting, herunder hvor stor den meteoroider (de faste dele af interplanetarisk affald, der zipper gennem rummet) er, hvor hurtigt de bevæger sig, i hvilken vinkel de kommer ind i atmosfæren osv. Men lad os kalde det 100 km.
Det tætteste en meteor kan være på dig er, hvis du er direkte under den, og så er det 100 km lige op (på din højde). Hvis det brænder længere væk fra zenit, så må det være længere fra dig. Længst væk kan du se en meteor, det er fornuftigt, er derfor, hvis det er lige i horisonten.
Geometrien ser sådan ud (bemærk: IKKE i skala):
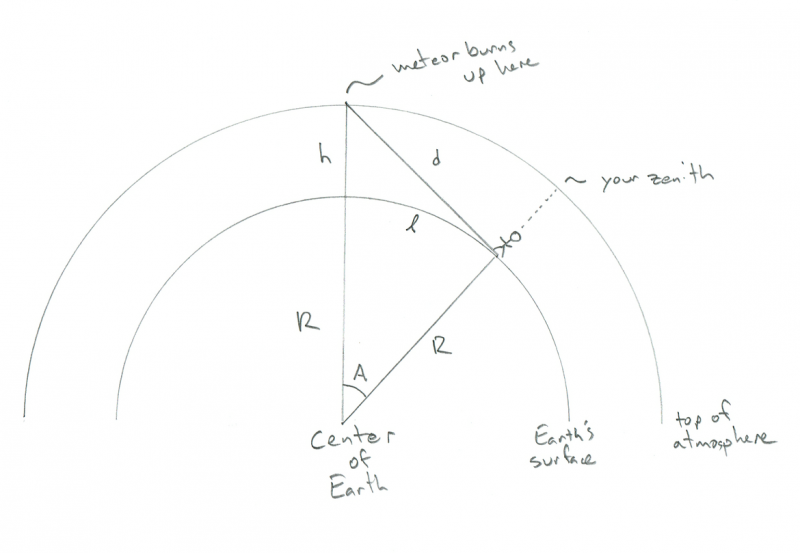
Skematisk viser geometrien af en observatør, der ser en meteor brænde op. Kredit: Phil Plait
Du kan se den lille pindfigur, der står på overfladen af den buede jord - lad os sige, at det er dig - med den (også buede) atmosfære over sig. I dette diagram er R jordens radius (6.4000 km), h er den højde, meteoren brænder op (100 km), og d er afstanden fra dig til meteoren. A er vinklen mellem din position på Jorden og meteorens position over den, og kursiv l (som i længden) er den afstand, du skal gå for at få meteoren til at være direkte overhead (jeg ved, at det virker som en underlig ting at ville vide det, men tål med mig). Mærkeligt nok kan du beregne alt, hvad du har brug for her uden at kende d, men jamen, det er fedt at vide, hvor langt væk meteoren er, ikke?
Nøglen til alt dette er at se, at vinklen mellem meteoren, dig og Jordens centrum er en ret vinkel. Det er fordi meteoren er i horisonten set af dig (eller, hvis du foretrækker sjov jargon, på tangentlinjen på den inderste cirkel, hvor R skærer den). Det gør trekanten til en rigtig trekant, og hvis du husker din gymnasial matematik, betyder det, at du kan finde alle sider og vinkler!
Husk den pythagoranske sætning ? I en højre trekant er kvadratet af hypotenusens længde lig med summen af firkanterne på de to andre sider*. I vores trekant er hypotenusen R+h, og de andre sider er R og d.
Så
(R+h)2= d2+ R2
eller multiplicere i venstre side (brug FOIL ):
R2+ 2Rh + h2 = d2+ R2
Løs for d for at se, hvor langt væk meteoren er fra dig. Bemærk, at R2 er på begge sider, så aflys dem for at få
d2= 2Rh + h2
Eller
d = kvadratrod (2Rh + h2)
Vi kender alle disse tal! Plug-n-chug, baby:
d = kvadratrod (2 x 6.400 x 100 + 10.000) = 1.136 km
Aha! Det betyder, at hvis du ser en meteor i horisonten, er den over 1.100 kilometer væk! Det er langt, og teknisk set længst væk kan du se en meteor fra jorden.
Lad os nu finde kursiv l. Først skal vi kende vinklen A. Det kræver en vis trigonometri. Der er mange trig identiteter du kan bruge til at finde ud af dette, men min favorit†er, at i en retvinklet trekant er sinus for en vinkel længden på den modsatte side divideret med længden af hypotenusen. Så hvis vi får dette forhold, kan vi tage den inverse sinus (eller buehorn) for at få vinklen.
sin (A) = d / (R + h)
så
A = uden-1(d / R + h)
Plug-n-chug igen, og jeg får A = 10 °. Det er en anstændig del af Jordens overflade!
Og nu kan vi få kursiv l. Der er 360 ° rundt om Jorden, og Jordens omkreds er 2 x pi x radius = 40.192 km, så der er
drengen, der udnyttede vinden
40.192 km / 360 ° = 112 kilometer i grader
hvilket igen betyder 10 ° = 1.120 kilometer. Det er ret tæt på d, hvilket ikke er for overraskende. Tegningerne er overdrevne, men i virkeligheden er luftskallen over os lille i forhold til Jordens størrelse. Hvis jeg lavede tegningerne i målestok, ville du se, at d og l virkelig er ret tæt på længden.
Okay, hvorfor er jeg så varm og generet over at finde l? På grund af det oprindelige spørgsmål! Hvis du efter al den matematik har glemt, hvor langt væk kan to mennesker være og stadig se den samme meteor?
I så fald ville meteoren være direkte mellem dem og på hver deres respektive horisont. Denne geometri ser sådan ud:
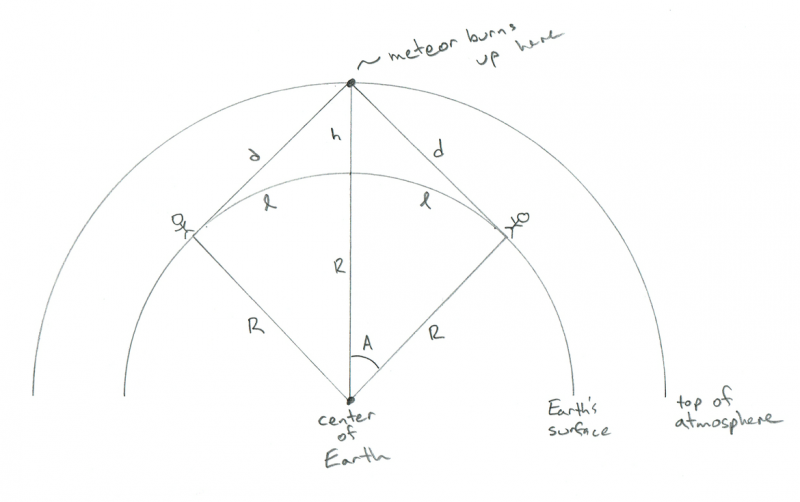
Skematisk viser geometrien for to observatører, der ser en meteor, der brænder præcis op mellem dem. Kredit: Phil Plait
AHA! Nu kan du se, hvorfor jeg vil have l! Afstanden mellem de to personer er kun 2 x l! Så nu har vi svaret:
række uheldige begivenheder bog 1
For at to mennesker kan se den samme meteor, kan de ikke være mere end 2 x 1.120 = 2.240 kilometer fra hinanden. Som et eksempel er det temmelig tæt på afstanden mellem Washington, DC og Denver. Wow.
For en ændring af perspektiv (bogstaveligt talt) betyder dette i øvrigt fra meteorens synspunkt, at det kan se en strækning af jorden 2.240 kilometer bred (som i, DC på Jordens østlige lem og Denver på den vestlige). Det er ret sejt.
Og det bringer os til det egentlige svar på Deans spørgsmål: Hvis han var 1.000 km fra sin familie, så ja, teknisk set kunne de se den samme meteor. Hvad med det?
Nu antager dette igen, at luften er helt klar og alt det, som i virkeligheden er i det væsentlige umuligt. Så denne matematik repræsenterer en ideel situation (herunder ideen om, at meteoren er præcis mellem dem).
Lad os være mere realistiske. Lad os sige, at meteoren brænder op på himlen i en højde af 45 ° over horisonten for begge observatører. Hvor langt væk ville de være fra hinanden? Nå igen, forudsat at meteoren er præcis mellem dem, er geometrien mere sådan:
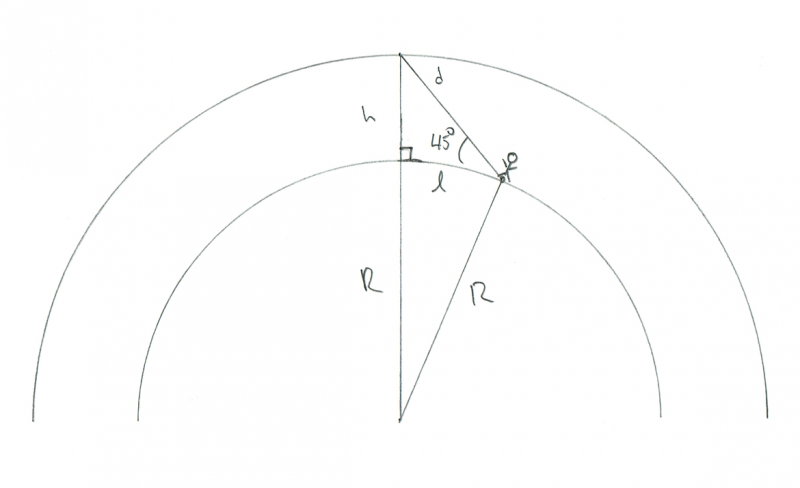
Skematisk viser geometrien af en observatør, der ser en meteor, der brænder 45 ° over horisonten. Kredit: Phil Plait
Dette er faktisk sværere at løse, men jeg kender et andet trick: Hvis vi antager, at l er lille, så vil Jordens krumning ikke være vigtig. For eksempel, hvis jeg vil vide afstanden mellem to træer i min gård, er jeg ligeglad med, at Jorden er buet. Over sådan en lille afstand kan jeg gå ud fra, at den er flad. Lad os tage den antagelse her.
I så fald har vi en anden retvinklet trekant, men denne gang er den rigtige vinkel den under meteoren. Jeg har endda mærket det i diagrammet med den lille firkantede notation. Så hvis det er en 90 ° vinkel, og vores vinkel til meteoren er 45 °, så er den sidste vinkel (fra meteoren til observatøren) også 45 °. Det betyder, at dette skal være en ensartet trekant, så l og h er de samme! Da vi ved, at h er 100 km, så må l.
Og det betyder, at afstanden mellem vores to observatører er det dobbelte, eller 200 km.
I øvrigt er afstanden til meteoren i dette tilfælde cirka 141 km. Jeg overlader at bekræfte det som en øvelse til læseren.
I princippet betyder det, at hvis du ved, hvor højt fra horisonten en meteor er, og den højde, som den brændte op, kan du beregne dens afstand (eller hvis du kender afstanden, kan du få dens højde). Den trig er dog temmelig kompliceret, og jeg synes, jeg har kastet nok matematik til dig i dag.
Men det er fedt at tænke på, at en lille smule gymnasial matematik kan have sådan en sjov applikation. Og jeg indrømmer, at det er poetisk og romantisk at vide, at så længe adskillelsen ikke er for langt, er det muligt at dele at se et stjerneskud med en anden. Hvilken dejlig tanke.
* I Troldmanden fra Oz , fik fugleskræmsel dette forkert efter han fik en hjerne.
† Af Rute Jeg har en yndlings trig -identitet. Hvad er din?